Scala Cats comes with a rich set of typeclasses, each of which “owns” a well-defined autonomous problem space. Many of those typeclasses are correlated and some are extended from others.
In this blog post, we’re going to give an at-a-glance hierarchical view of some of the most common Cats typeclasses. For brevity, we’ll skip discussions re: their corresponding mathematical laws, which can be found in many relevant tech docs. Our focus will be more on highlighting the correlations among these typeclasses.
Common typeclass hierarchy
For the impatient, below is a diagram highlighting the hierarchical correlation.
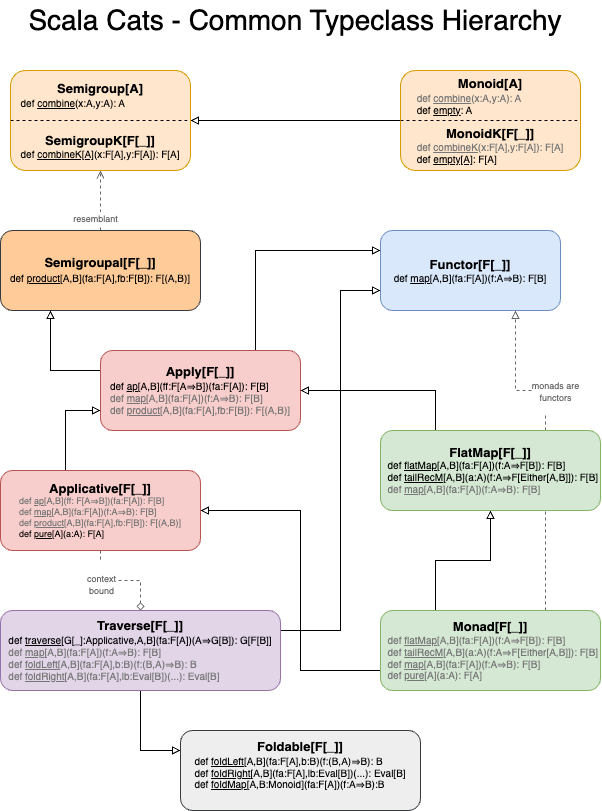
Semigroup and Monoid
Let’s start with the simplest ones, Semigroup and Monoid.
Semigroup comes with the abstract method combine to be implemented with the specific “combine” computational logic such as the addition of integers, union of sets, etc.
trait Semigroup[A] {
def combine(x: A, y: A): A
}
trait Monoid[A] extends Semigroup[A] {
def combine(x: A, y: A): A
def empty: A
}
Note that Monoid simply supplements Semigroup with empty as the “zero” or “identity” element, allowing aggregating operations of arbitrarily many elements (e.g. summation of numbers from an initial 0).
Example:
implicit def setSemigroup[A]: Semigroup[Set[A]] =
new Semigroup[Set[A]] {
def combine(s1: Set[A], s2: Set[A]) = s1 union s2
}
// Or, using SAM for brevity
// implicit def setSemigroup[A]: Semigroup[Set[A]] = _ union _
val setSG = implicitly[Semigroup[Set[Char]]]
setSG.combine(Set('a', 'b'), Set('c'))
// Set('a', 'b', 'c')
implicit def setMonoid[A](implicit sg: Semigroup[Set[A]]): Monoid[Set[A]] =
new Monoid[Set[A]] {
def combine(s1: Set[A], s2: Set[A]) = sg.combine(s1, s2)
def empty = Set()
}
val setM = implicitly[Monoid[Set[Char]]]
List(Set('a','b'),Set('c'),Set('d','e')).
foldLeft(setM.empty)(setM.combine(_, _))
// HashSet('e', 'a', 'b', 'c', 'd')
SemigroupK and MonoidK
With a similar correlation, SemigroupK and MonoidK are the higher-kinded version of Semigroup and Monoid, respectively. SemigroupK combines values within a given context and MonoidK ensures the existence of an “empty” context.
trait SemigroupK[F[_]] {
def combineK[A](x: F[A], y: F[A]): F[A]
}
trait MonoidK[F[_]] extends SemigroupK[F] {
def combineK[A](x: F[A], y: F[A]): F[A]
def empty[A]: F[A]
}
Example:
implicit val listSemigroupK: SemigroupK[List] =
new SemigroupK[List] {
def combineK[A](ls1: List[A], ls2: List[A]) = ls1 ::: ls2
}
val listSGK = implicitly[SemigroupK[List]]
listSGK.combineK(List(1,2), List(3))
// List(1, 2, 3)
implicit def listMonoidK(implicit sgk: SemigroupK[List]): MonoidK[List] =
new MonoidK[List] {
def combineK[A](ls1: List[A], ls2: List[A]) = sgk.combineK(ls1, ls2)
def empty[A] = List.empty[A]
}
val listMK = implicitly[MonoidK[List]]
List(List(1,2),List(3),List(4,5)).foldLeft[List[Int]](listMK.empty)(listMK.combineK(_, _))
// List(1, 2, 3, 4, 5)
Functor
Functor is a higher-kinded typeclass characterized by its method map which transforms some value within a given context F via a function.
trait Functor[F[_]] {
def map[A, B](fa: F[A])(f: A => B): F[B]
}
Example:
implicit val listFunctor: Functor[List] =
new Functor[List] {
def map[A, B](ls: List[A])(f: A => B) = ls.map(f)
}
val listF = implicitly[Functor[List]]
listF.map(List(1,2,3))(i => s"#$i!")
// List("#1!", "#2!", "#3!")
Monad
Monad enables sequencing of operations in which resulting values from an operation can be utilized in the subsequent one.
But first, let’s look at typeclass FlatMap.
trait FlatMap[F[_]] extends Apply[F] {
def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B]
def map[A, B](fa: F[A])(f: A => B): F[B]
@tailrec
def tailRecM[A, B](init: A)(f: A => F[Either[A, B]]): F[B]
}
FlatMap extends Apply whose key methods aren’t what we would like to focus on at the moment. Rather, we’re more interested in method flatMap which enables sequential chaining of operations.
In addition, method tailRecM is a required implementation for stack-safe recursions on the JVM (which doesn’t natively support tail call optimization).
Monad inherits almost all its signature methods from FlatMap.
trait Monad[F[_]] extends FlatMap[F] with Applicative[F] {
def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B]
def pure[A](a: A): F[A]
def map[A, B](fa: F[A])(f: A => B): F[B]
@tailrec
def tailRecM[A, B](init: A)(f: A => F[Either[A, B]]): F[B]
}
Monad also extends Applicative which we’ll get to (along with Apply) in a bit. For now, it suffices to note that Monad inherits pure from Applicative.
Even without realizing that Monad extends Functor (indirectly through FlatMap and Apply), one could conclude that Monads are inherently Functors by implementing map using flatMap and pure.
def map[A, B](fa: F[A])(f: A => B): F[B] = flatMap(fa)(a => pure(f(a)))
Example:
trait Monad[F[_]] { // Skipping dependent classes
def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B]
def pure[A](a: A): F[A]
def map[A, B](fa: F[A])(f: A => B): F[B]
def tailRecM[A, B](init: A)(f: A => F[Either[A, B]]): F[B]
}
implicit val optionMonad: Monad[Option] =
new Monad[Option] {
def flatMap[A, B](opt: Option[A])(f: A => Option[B]) = opt.flatMap(f)
def pure[A](a: A) = Option(a)
def map[A, B](opt: Option[A])(f: A => B): Option[B] = flatMap(opt)(a => pure(f(a)))
@scala.annotation.tailrec
def tailRecM[A, B](a: A)(f: A => Option[Either[A, B]]): Option[B] = f(a) match {
case None => None
case Some(leftOrRight) => leftOrRight match {
case Left(a1) => tailRecM(a1)(f)
case Right(b1) => Option(b1)
}
}
}
val optMonad = implicitly[Monad[Option]]
optMonad.flatMap(Option(3))(i => if (i > 0) Some(s"#$i!") else None)
// Some("#3!")
Semigroupal and Apply
A higher-kinded typeclass, Semigroupal conceptually deviates from SemiGroup’s values combining operation to joining independent contexts in a tupled form “product”.
trait Semigroupal[F[_]] {
def product[A, B](fa: F[A], fb: F[B]): F[(A, B)]
}
Despite the simplicity of method product (which is the only class method), Semigroupal lays out the skeletal foundation for the problem space of concurrency of independent operations, as opposed to Monad’s sequential chaining.
Next, Apply brings together the goodies of Semigroupal and Functor. Its main method ap has a rather peculiar signature that doesn’t look intuitively meaningful.
trait Apply[F[_]] extends Semigroupal[F] with Functor[F] {
def ap[A, B](ff: F[A => B])(fa: F[A]): F[B]
def map[A, B](fa: F[A])(f: A => B): F[B]
def product[A, B](fa: F[A], fb: F[B]): F[(A, B)]
}
Conceptually, it can be viewed as a specialized map in which the transformation function is “wrapped” in the context.
By restructuring the type parameters in ap[A, B] and map[A, B], method product can be implemented in terms of ap and map.
// 1: Substitute `B` with `B => (A, B)` def map[A, B](fa: F[A])(f: A => B => (A, B)): F[B => (A, B)] // 2: Substitute `A` with `B` and `B` with `(A, B)` def ap[A, B](ff: F[B => (A, B)])(fb: F[B]): F[(A, B)] // Applying 1 and 2: def product[A, B](fa: F[A], fb: F[B]): F[(A, B)] = ap(map(fa)(a => (b: B) => (a, b)))(fb)
Applicative
trait Applicative[F[_]] extends Apply[F] {
def pure[A](a: A): F[A]
}
Like how Monoid supplements SemiGroup with the empty element to form a more “self-contained” typeclass, Applicative extends Apply and adds method pure which wraps a value in a context. The seemingly insignificant inclusion makes Applicative a typeclass capable of addressing problems within a particular problem space.
Similarly, Monad takes pure from Applicative along with the core methods from FlatMap to become another “self-contained” typeclass to master a different computational problem space.
Contrary to Monad’s chaining of dependent operations, Applicative embodies concurrent operations, allowing independent computations to be done in parallel.
We’ll defer examples for Applicative to a later section.
Foldable
Foldable offers fold methods that go over (from left to right or vice versa) some contextual value (oftentimes a collection) and aggregate via a binary function starting from an initial value. It also provides method foldMap that maps to a Monoid using an unary function.
trait Foldable[F[_]] {
def foldLeft[A, B](fa: F[A], b: B)(f: (B, A) => B): B
def foldRight[A, B](fa: F[A], lb: Eval[B])(f: (A, Eval[B]) => Eval[B]): Eval[B]
def foldMap[A, B: Monoid](fa: F[A])(f: A => B): B
}
Note that the well known foldRight method in some Scala collections may not be stack-safe (especially in older versions). Cats uses a data type Eval in its foldRight method to ensure stack-safety.
Traverse
Traverse extends Functor and Foldable and provides method traverse. The method traverses and transforms some contextual value using a function that wraps the transformed value within the destination context, which as a requirement, is bound to an Applicative.
trait Traverse[F[_]] extends Functor[F] with Foldable[F] {
def traverse[G[_]: Applicative, A, B](fa: F[A])(ff: A => G[B]): G[F[B]]
}
If you’ve used Scala Futures, method traverse (and the sequence method) might look familiar.
def sequence[G[_]: Applicative, A](fg: F[G[A]]): G[F[A]] = traverse(fg)(identity)
Method sequence has the effect of turning a nested context “inside out” and is just a special case of traverse by substituting A with G[B] (i.e. making ff an identity function).
Example: Applicative and Traverse
To avoid going into a full-on implementation of Traverse in its general form that would, in turn, require laborious implementations of all the dependent typeclasses, we’ll trivialize our example to cover only the case for Futures (i.e. type G = Future).
First, we come up with a specialized Traverse as follows:
import scala.concurrent.{ExecutionContext, Future}
trait FutureTraverse[F[_]] { // Skipping dependent classes
def traverse[A, B](fa: F[A])(ff: A => Future[B]): Future[F[B]]
}
For similar reasons, let’s also “repurpose” Applicative to include only the methods we need. In particular, we include method map2 which will prove handy for implementing the traverse method for FutureTraverse.
trait Applicative[F[_]] { // Skipping dependent classes
def map[A, B](fa: F[A])(f: A => B): F[B]
def map2[A, B, Z](fa: F[A], fb: F[B])(f: (A, B) => Z): F[Z]
def pure[A](a: A): F[A]
}
implicit val futureApplicative: Applicative[Future] =
new Applicative[Future] {
implicit val ec = ExecutionContext.Implicits.global
def map[A, B](fa: Future[A])(f: A => B): Future[B] = fa.map(f)
def map2[A, B, Z](fa: Future[A], fb: Future[B])(f: (A, B) => Z): Future[Z] =
(fa zip fb).map(f.tupled)
def pure[A](a: A): Future[A] = Future.successful(a)
}
We implement map2 by tuple-ing the Futures and binary function via zip and tupled, respectively. With the implicit Applicative[Future] in place, we’re ready to implement FutureTraverse[List].
implicit val listFutureTraverse: FutureTraverse[List] =
new FutureTraverse[List] {
implicit val ec = ExecutionContext.Implicits.global
implicit val appF = implicitly[Applicative[Future]]
def traverse[A, B](ls: List[A])(ff: A => Future[B]): Future[List[B]] = {
ls.foldRight[Future[List[B]]](Future.successful(List.empty[B])){ (a, acc) =>
appF.map2(ff(a), acc)(_ :: _)
}
}
}
import scala.concurrent.ExecutionContext.Implicits.global
val lsFutTraverse = implicitly[FutureTraverse[List]]
lsFutTraverse.traverse(List(1,2,3)){ i =>
if (i > 0) Future.successful(s"#$i!") else Future.failed(new Exception())
}
// Future(Success(List("#1!", "#2!", "#3!")))
As a side note, we could implement traverse without using Applicative. Below is an implementation leveraging Future’s flatMap method along with a helper function (as demonstrated in a previous blog post about Scala collection traversal).
implicit val listFutureTraverse: FutureTraverse[List] =
new FutureTraverse[List] {
implicit val ec = ExecutionContext.Implicits.global
def pushToList[A](a: A)(as: List[A]): List[A] = a :: as
def traverse[A, B](ls: List[A])(ff: A => Future[B]): Future[List[B]] = {
ls.foldRight[Future[List[B]]](Future.successful(List.empty[B])){ (a, acc) =>
ff(a).map(pushToList).flatMap(acc.map)
}
}
}
