An outlet of thoughts and insights by Leo Cheung on scalable contemporary software technology on distributed computing platforms, with proof-of-concept applications using Scala, Akka, Apache Spark, Kafka, SQL/NoSQL, AWS.
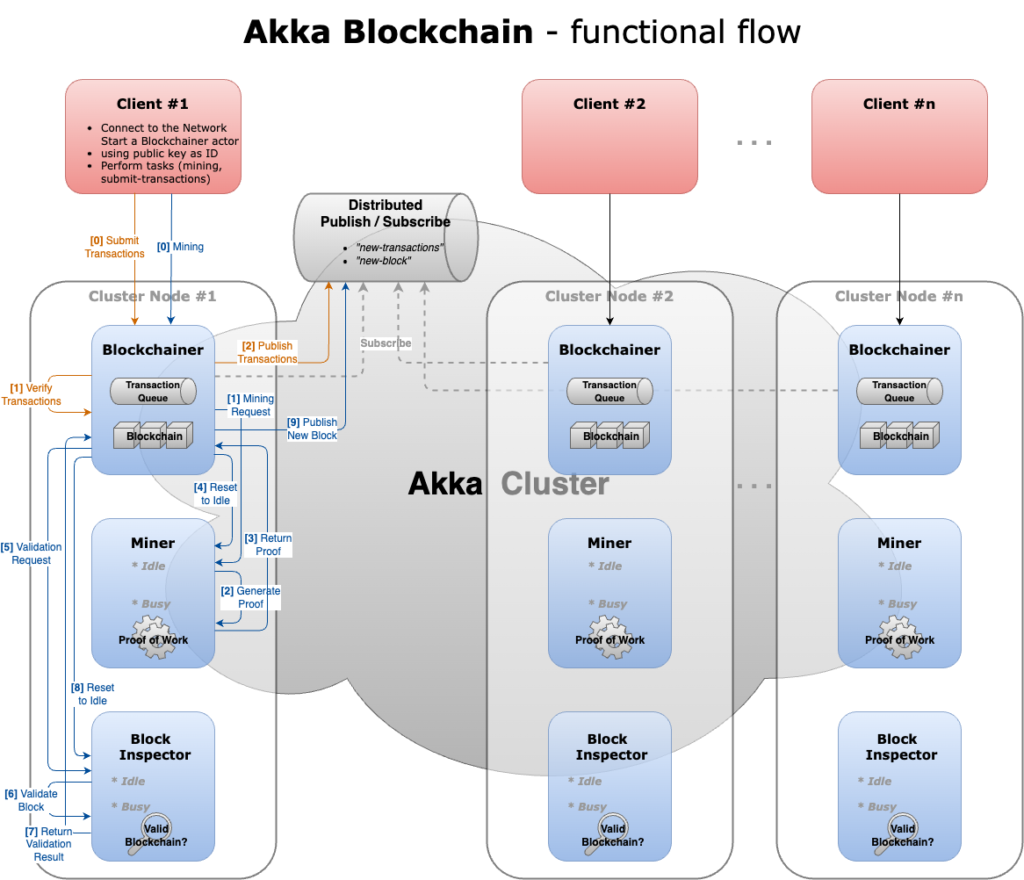
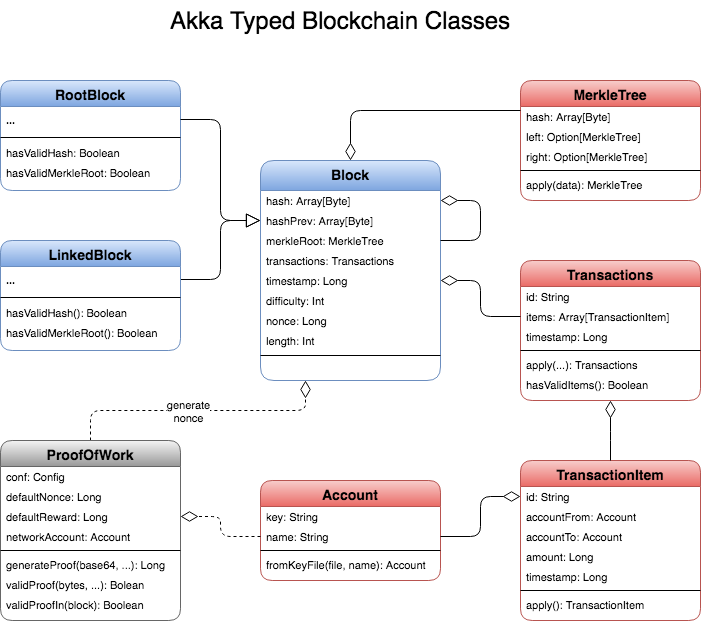
Blockchain & Akka Actor
- A Brief Overview Of Blockchains
- Actor-based Blockchain In Akka Typed
- Akka Typed Actors (series)
- Blockchain With Akka Actors (series)
- Smart Contract DApps
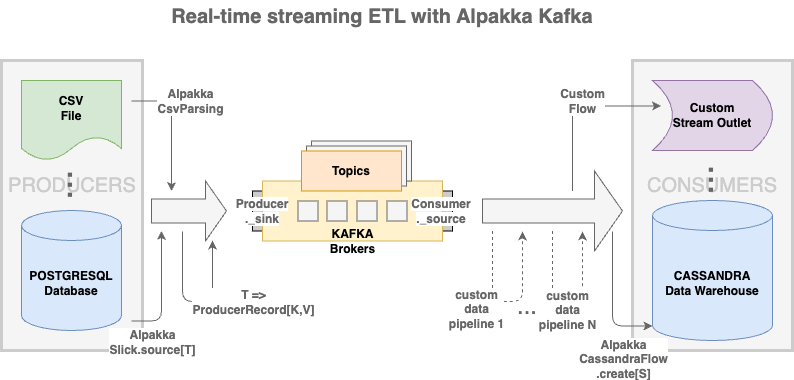
Streaming ETL & Akka Stream
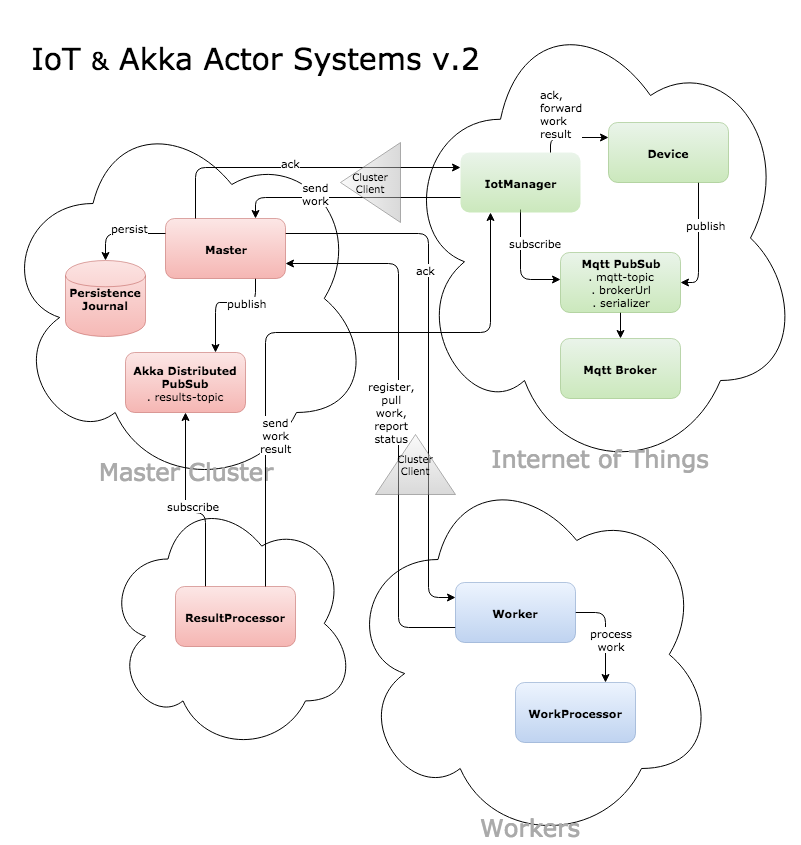
Internet-of-Things
- Actor-based IoT
- gRPC Streaming (series)
- Scala Distributed Systems With Akka
- Home Area Network
Scala
- Reactor Pattern with NIO
- Trampolining with Scala TailCalls
- Traversing A Scala Collection
- Scala Unfold
- Polymorphism and Typeclasses
- Composing Partial Functions In Scala
- Fibonacci In Scala: Tailrec, Memoized
- Scala Futures (series)
- Implicit Conversion In Scala
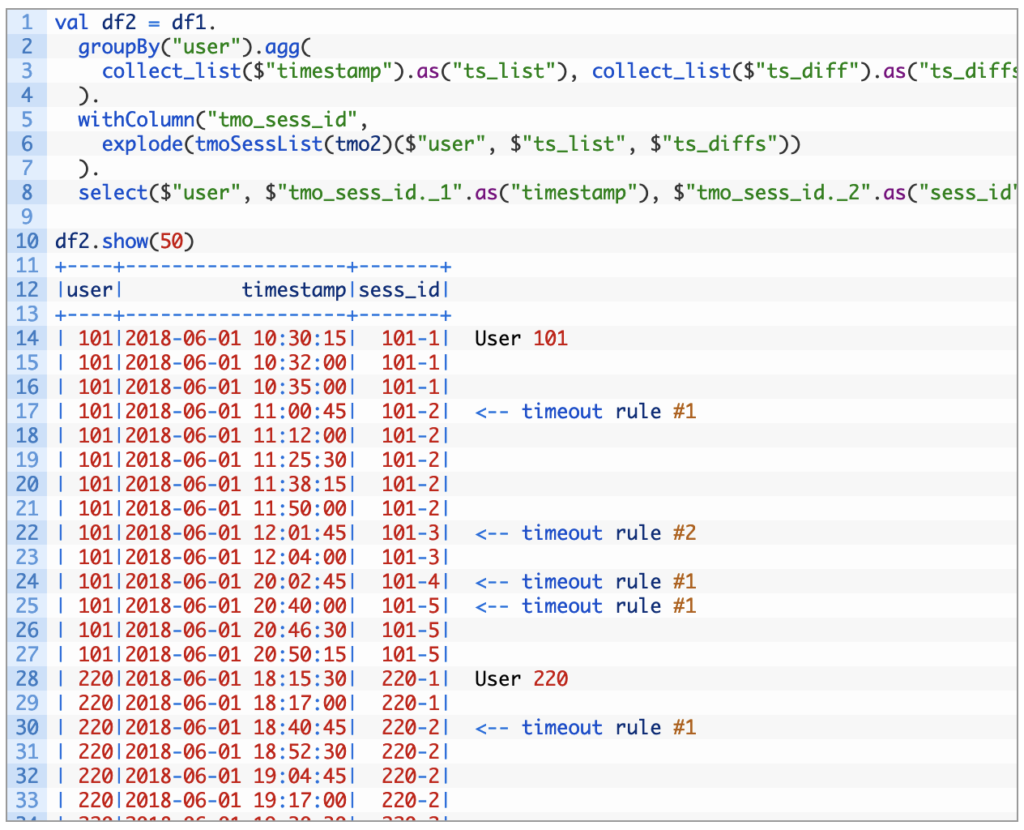
Apache Spark
- Spark Higher-order Functions
- Spark Schema With Nested Columns
- Time Series Spark (series)
- Scala on Spark (series)

Startup Ventures
Algorithm & Game